Элементы зонной теории твердого тела , страница 7
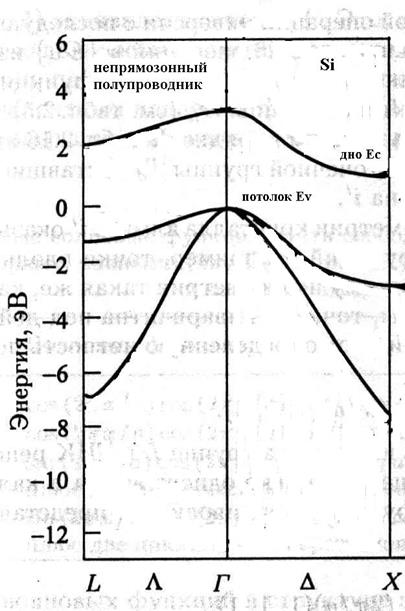
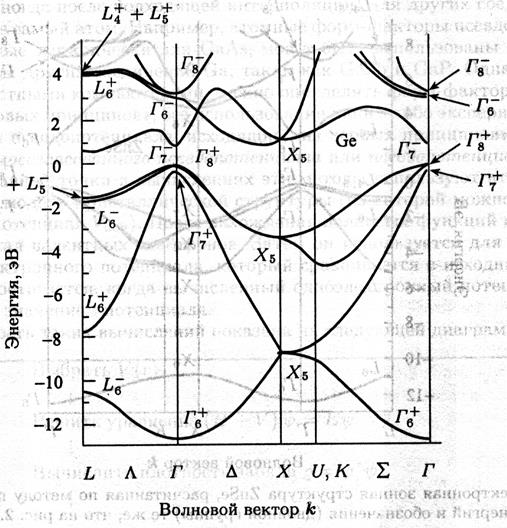
Рис. 3.6. Упрощённая зонная структура Si (слева) и зонная структура Ge (справа), данные из книги 2.1.
На рисунках 3.4 и 3.6 приведена структура энергетических зон для арсенида галлия, кремния и германия. Потолок валентной зоны, и дно зоны проводимости в GaAs (рис. 3.4) находятся в точке G (прямозонный материал), ширина запрещённой зоны составляет 1.43 эВ (при комнатной температуре). Эффективная масса для электронов изотропна и составляет 0.067 (и здесь и далее мы будем соотносить эффективную массу к массе свободного электрона). Валентная зона содержит: 1) зону тяжёлых дырок; 2) зону легких дырок; 3) отщеплённую за счет спин-орбитального взаимодействия зоны. Каждая из трёх зон двукратно вырождена по спину. Масса тяжёлых дырок составляет 1.12, масса лёгких дырок 0.5. Дисперсия дырок в GaAs непараболична (см. рис. 3.5). Кстати «близкий родственник» арсенида галлия и его постоянный партнёр по гетероструктурам – AlAs является непрямозонным полупроводником.
Кремний и германий являются непрямозонными материалами (рис.3.6). В кремнии дно зоны проводимости находится на направлении D зоны Бриллюэна (не на границе зоны). Таким образом, электроны в кремнии заселяют 6 X долин. Ширина запрещённой зоны кремния — 1.1 эВ при комнатной температуре. Эффективная масса электронов X-долины в кремнии анизотропна, изоэнергетическая поверхность – эллипсоид вращения, вытянутый вдоль главных кристаллографических направлений. Продольная (тяжёлая) масса составляет 0.97, две поперечных массы равны 0.19. Массы тяжёлых и легких дырок составляют 0.5 и 0.16 соответственно.
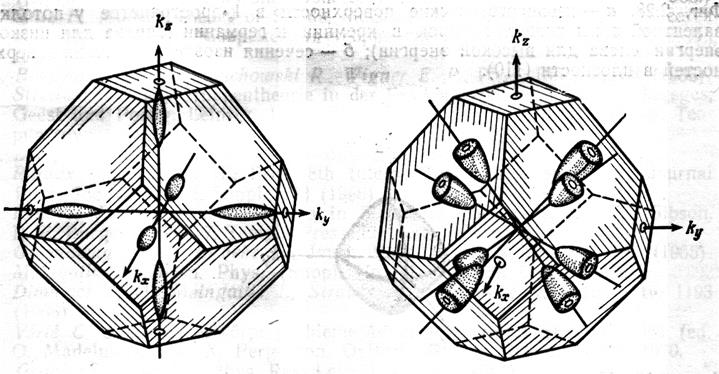
В германии дно зоны проводимости находится на направлении L зоны Бриллюэна, на границе зоны в точке L. Таким образом, электроны в германии заселяют 8 половинок L долин (всего 4 L долины). Ширина запрещённой зоны германия — 0.66 эВ при комнатной температуре. Эффективная масса электронов L-долины в германии также анизотропна, изоэнергетическая поверхность также эллипсоид вращения, вытянутый вдоль семейства эквивалентных кристаллографических направлений. Продольная масса составляет 1.58, две поперечных массы равны 0.082. Массы тяжёлых и легких дырок составляют 0.3 и 0.04 соответственно. Изоэнергетические поверхности для электронов в кремнии и германии показаны на рисунке 3.7.
Рис. 3.7. Изоэнергетические поверхности долин электронов в кремнии (слева) и германии (справа).
Существуют оптические и электрофизические методики исследования энергетического спектра. Рассмотрим некоторые из них. Существование провала в энергетических уровнях (запрещённой зоны) приводит к возникновению оптической щели в поглощении света. Фотоны с энергией меньше чем ширина запрещённой зоны не могут возбудить электрон из валентной зоны в зону проводимости и не поглощаются кристаллом, то есть существует край поглощения. По положению края поглощения можно судить о ширине запрещённой зоны. При испускании света в процессе релаксации электрона с возбуждённого состояния вблизи дна зоны проводимости в валентную зону, энергия излучаемого фотона также соответствует ширине запрещённой зоны. То есть, используя данные фотолюминесценции, можно судить о ширине Eg. Тут главное различать переходы зона проводимости — валентная зона (так называемые фундаментальные переходы) от оптических переходов, связанными с примесями (дающими состояния в запрещённой зоне). Исследуя распределения по энергии (энергетический спектр) электронов, испускаемых кристаллом при освещении потоком фотонов (внешний фотоэффект), можно исследовать плотность состояний в валентной зоне. Тензор эффективной массы можно исследовать по резонансному поглощению по СВЧ-излучения в кристаллах в сильном магнитном поле. Резонанс имеет место, когда частота СВЧ-излучения совпадает с циклотронной частотой (циклотронный резонанс [1.7]). Этот эффект имеет как классическое, так и квантово-механическое объяснение. Циклотронная частота зависит от соотношения заряда к массе, и, в случае анизотропии эффективной массы, будет зависеть от направления магнитного поля.
Более подробно о методиках исследования зонной структуры можно прочитать в книгах 2.1-2.6.
1) Нарисовать сечение изоэнергетической поверхности плоскостью (001) для электронов в кремнии. Показать направление продольной и поперечной массы.
2) Найти, при каком магнитном поле энергия циклотронного резонанса 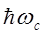
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им. Даля 166
- ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им. Дегтярева 174
- КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им. Макарова 543
- НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им. Герцена 123
- РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им. Гагарина 114
- СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им. Каразина 305
- ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Полный список ВУЗов
Чтобы распечатать файл, скачайте его (в формате Word).
Источник
При расчетах плотности состояний в зонах Бриллюэна со сложной поверхностью
Таким образом, плотность состояний у дна и потолка зон имеет совершенно аналогичный вид, поскольку найденные выражения для N(Е) являются следствием квадратичной зависимости энергии от квазиимпульса в окрестности экстремумов, различный знак подкоренного выражения — E-Ec и Ev-E — является следствием различия в знаках эффективной массы в минимуме и максимуме энергии.
А где же сложность расчетов, о которой мы говорили в начале раздела? Основные трудности при расчете плотности состояний в зонах Бриллюэна реальных полупроводников возникает:
— при расчете плотности состояний в узкозонных полупроводниках, где требуется учет отклонения от параболической зависимости энергии от волнового вектора,
— при определении эффективных масс плотности состояний,
В качестве примера рассмотрим расчет эффективных масс плотности состояний для электронов и дырок в классических полупроводниковых материалах: кремнии и германии.
Для этого вспомним следующее (глава 1). Кремний и германий имеют кристаллическую решетку типа алмаза, представляющую собой две гранецентрированные кубические решетки, сдвинутые одна относительно другой на ¼ пространственной диагонали. Для них первая зона Бриллюэна имеет форму четырнадцатигранника, изображенного на рис. 1.43, шесть граней которого имеют форму квадрата, а восемь – шестиугольника. Первая зона Бриллюэна, вписанная в элементарную ячейку обратной решетки для Si и Ge показана на рис. 1.55. Внутри этого многогранника (зоны Бриллюэна) энергия является непрерывной (точнее непрерывной функцией волнового вектора к), а на границах зоны наблюдается разрыв энергии как функции к.
Кремний. Рассматривая зонную структуру кремния, мы отмечали, что всего в первой зоне Бриллюэна располагается шесть минимумов. Форма поверхностей постоянной энергии в зоне проводимости кремния представляют собой шесть эллипсоидов, вытянутых вдоль главных кристаллографических осей (рис. 1.55). Значения компонент тензора эффективной массы электрона, определенные по циклотронному резонансу, составляют у кремния m1=m2=mt = 0,19m0, m3=ml=0,92m0. Величина эффективной массы электронов для плотности состояний, рассчитанная на основании соотношения (2.23) с учетом значения числа эллипсоидов М=6, будет равна 1,08m0.
Следовательно, у кремния все шесть эллипсоидов изоэнергетической поверхности зоны проводимости можно заменить одной сферической поверхностью с эффективной массой плотности состояний для электронов, равной 1,08m0.
Сложнее обстоит дело с расчетом эффективной массы дырок для плотности состояний. В центре зоны Бриллюэна валентная зона дважды вырождена (рис.1.52). Поверхность равной энергии представляет собой гофрированные (то есть деформированные сферы) поверхности (см. рис.1.56). Для легких дырок поверхность незначительно отличается от сферы, а для тяжелых дырок она более деформирована. Однако и в том и другом случае приближенно их можно аппроксимировать двумя сферическими поверхностями, которым соответствуют эффективные массы тяжелых mpт и легких mpл дырок. В этом случае плотность состояний (с учетом спина) будет определяться суммой плотности состояний в зонах тяжелых и легких дырок:
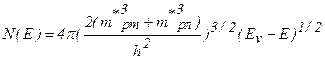
Изоэнергетические поверхности обеих зон можно заменить одной приведенной сферой с плотностью состояний
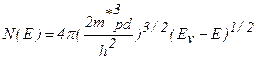
для которой эффективная масса плотности состояний для дырок равна
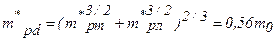
так как из экспериментов по циклотронному резонансу найдены следующие значения эффективных масс тяжелых и легких дырок:
Германий. В первой зоне Бриллюэна германия имеется восемь минимумов энергии, расположенных в точках [1/2, 1/2, 1/2]. Cоответствующие поверхности равной энергии изображены на рис. 1.55 и имеют, как и в кремнии, форму элипсоидов. Однако в отличие от кремния, эти восемь эллипсоидов рассечены пополам гранями зоны Бриллюэна (т.е. одна половина каждого эллипсоида принадлежит первой зоне Бриллюэна, а вторая половина – второй зоне Бриллюэна). Поэтому в основной (первой) зоне Бриллюэна германия расположены восемь половинок эллипсоидов или, что эквивалентно, четыре полных эллипсоида (т.е. M=4), для которых m1=m2=mt = 0,082m0, m3=ml=1,59m0. Следовательно, плотность состояний для дна зоны проводимости германия будет определяться выражением (2.24) с эффективной массой плотности состояний для электронов, равной:
Cтруктура валентной зоны германия подобна структуре зоны кремния (рис.1.52, 1.56). Эффективная масса плотности состояний для дырок, характеризующая плотность квантовых состояний у потолка валентной зоны германия, будет равна:
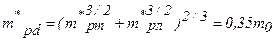
Арсенид галлия. Абсолютный минимум зоны проводимости лежит при k=0, а его поверхностями постоянной энергии являются сферы с центром в центре зоны Бриллюэна (рис.1.55). Поэтому эффективная масса электронов является скалярной величиной. Из экспериментов по циклотронному резонансу определена величина эффективной массы – 0,068m0. Следовательно, плотность состояний вблизи дна зоны проводимости арсенида галлия будет определяться выражением (2.24) с эффективной массой плотности состояний для электронов, равной:
Валентная зона арсенида галлия сходна с валентной зоной кремния. Поэтому расчет плотности состояний в валентной зоне проводится аналогично. Величина : 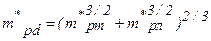
В заключение отметим следующее.
1. Выражения для плотности состояний в зоне проводимости и валентной зоне N(Е) справедливы до тех пор, пока применима квадратичная зависимость энергии от квазиимпульса. Для классических полупроводников (германий, кремний) основная часть носителей заряда располагается или вблизи дна зоны проводимости, или вблизи потолка валентной зоны, где такая зависимость энергии от квазиимпульса выполняется.
Вдали от границ зон выражение для N(E) не может быть записано в аналитическом виде, так как неизвестна зависимость E(к). Ход функции N(Е) в общем виде может быть весьма сложным. Для запрещенных зон N(Е) = 0, если не считать локализованных состояний электрона.

Плотность состояния для дискретных уровней можно выразить с помощью d-функции:
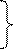 Nд(E)=Nдd(E-Eд), Na(E)=Nad(E-Ea), Nд(E)=Nдd(E-Eд), Na(E)=Nad(E-Ea), | (2.31) |
где через Nд(E), Nа(E) обозначена плотность состояний на донорном и акцепторном уровнях, характеризуемых энергией Eд и Eа соответственно. Если при возрастании концентрации примеси образуется примесная зона, то в этом случае выражения (2.31) не будут иметь места и должны быть заменены выражениями (2.24) или (2.28).
2. В случае параболического изотропного закона дисперсии эффективная масса, определяющая подвижность носителей заряда, и эффективная масса плотности состояний равны друг другу. В более общих случаях эти величины не совпадают. Результирующее значение эффективной масы, определяющее подвижность, получило названиеэффективной массы электропроводности, которую нужно отличать от эффективной массы плотности состояний. Так, например, в кремнии эффективная масса плотности состояний для электронов равна 1,08m0, тогда как эффективной массы электропроводности для электронов равна 0,26m0; результирующие эффективные массы для дырок соответственно равны 0,59m0 и 0,38m0.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник